小学数学：移动1根、2根火柴使等式成立，其实是有方法思路的!

在小学各个阶段学习中，尤其是低年级，有比较多的趣味题。教学设计的目的是让学生在游戏中学习，在学习中游戏，培养数学学习兴趣和提高数学思考能力。移动火柴就是其中经典的题型，将加减法的计算融入其中，除了考查学生对加减法计算的掌握程度，还加强了对学生图形数字的认识以及寻找办法的想象能力，对于学生逻辑思维能力的培养是非常突出的。

学生遇到移动火柴的题目，很多时候都不知道如何入手，像碰运气一样的去试，试对了只能说明运气好，下次再遇到，同样还是不会做。此种题目需要讲究一定的思考方法，不然就是盲目做题，效果不佳。

今天以几个题目为例，分享下如何进行思路的分析和方法的寻找，讲得会比较细，思路会有好几种，就看哪种方法学生容易接受。本文主要目的是讲解不同方法下的逻辑思考，这才是本题的落脚点，所以请各位保持耐心。

例题1：移动1根火柴棒，使下列等式成立

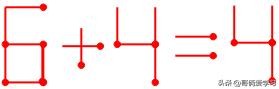
例题1

分析思路：

左边是加法，为6和4，右边是4，很明显左边大于右边。要使等式成立，思考方向是等号左边变小、等号右边变大或者等号右边不变。

1.等号左边变小：

1.1 加号变减号：这是最能够在第一时间想到的方法。我们拿走1根火柴将加法变为减法，等式变成6-4=4。然后思考拿走的1根火柴可以加到哪一个数字上，4加1根火柴不能变为任何数字（注意：9不行，需要2根火柴才可以），所以这根火柴只能加在6上，那就只能变为8，验证等式：8-4=4，等式成立。（或者这么想：不考虑4，直接观察6，加1根火柴，只能变为8，等式正好成立，得解）

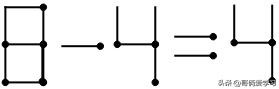
答案1

1.2 加号不变：左边的4加上或减去1根火柴都不能变为任何数字，所以只考虑数字6，左右两边都有4，还是加法，所以6需要变为0等式才成立，观察等式图形，发现只需将6中间的一横移动到右上即可变为0,0+4=4，等式成立。

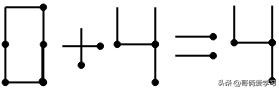
答案2

2.等号右边变大：上面已经分析过，只移动一根火柴的情况下，4不能变为其他数字，此方法行不通。

3.等号右边不变：面已经分等号右边不变，还是为4，要求左边加法变减法，和1.1情况一致，答案为8-4=4。

接下来讨论移动2根火柴进阶版题目的思考方向：

例题2:移动2根火柴棒，使下列等式成立：

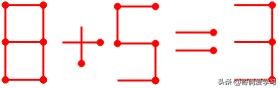
例题2

分析思路：

左边数字都比右边大，且包含8、5、3三个数字，由于本题是要移动2根火柴棒，所以思考方向可以是数字不变、等号左边变化以及等号右边变化三个维度之中的一个。

1.数字不变：

很容易想到3、5、8有一个等式关系：3+5=8。对照例题数字的位置可以变为8=5+3，由此联想将加法变为等号，等号变为加法，这样改变确实也只需要移动两根火柴棒，等式成立。

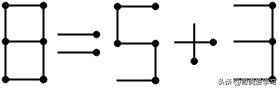
答案1

2.等号左边变化：

2.1 加号不变时：

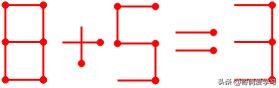
例题2

如果保持加号不变，左边数字肯定要减小，最多移动2根火柴棒的情况下，8能够减小为6、5、3、2、0

8变为6时：需要拿走8的一根火柴。右边的3只能是大于6的数，那就只能是8或者9（7不行是因为需要拿走2根才能变成7，而8变为6已经拿走一根了）。若3变为8，那么需要5在减少1根火柴的情况下变为2，无法满足；若3变为9，可指定该火柴棒来自8，于是需要5在移动1根自身火柴棒的情况下变为3，只需要将左边竖着的火柴棒平移到右边即可，答案为：6+3=9。

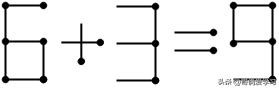
答案2

8变为5时：需要拿走8的2根火柴。于是3只能增加火柴棒，结合等式，只能变大为8或9或13。若3变为8或13，5就不能变化，等式不成立；若3变为9,5只能变为6或者9，6和9都不能使等式成立；因此，此种情况下没有答案。

8变为3时：需要拿走8的2根火柴。与上面同理，右边的3只能变大为8或9或13。若3变为8，5刚好不用移动火柴棒且等式成立，答案为：3+5=8；若3变为9，则需要5在增加1根火柴棒的情况下变为6，很明显，增加1根火柴棒到5左下即可，等式成立，答案为：3+6=9；若3变为13，5只能保持不变，但是等式不成立。

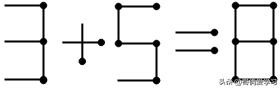
答案3

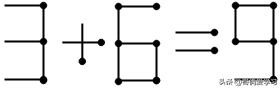
答案4

8变为2时：需要拿走8的2根火柴。与上面同理，右边3只能变大为8或9或13，此三种情况下，等式均不成立。

8变为0时：需要拿走8的1根火柴。然后5和3需要变为一样，我们看看5和3一共10根火柴，再加上从8那里拿来的1根，共11根火柴，不能分为两个相同的整数，所以该情况下等式均不成立。

2.2 加号变为减号:

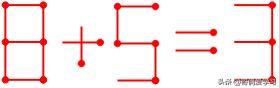
例题2

若加号变为减号，剩下的数字就只能移动1根了。下面讨论的方向可以从8入手，考虑8变化与否的两种情况：

若8不变：即题目变为8-（）=（），减数就不能大于8，于是5的变化就只能固定在8、6、5、3中。①若5变为8，需要从3中移出一根火柴给到5，3给出一根火柴后不代表任何数字，不成立；②若5变为6,则要求3在移动一根火柴的情况下变为2，可将3右下的竖线火柴平移到左下即可，满足条件，答案为：8-6=2；③若5不变，8-5就等于3,不满足移动2根火柴的要求，等式不成立；④若5变为3，可假定是由5左上竖线火柴平移到右上而来，那么加号里拿出来的火柴就只能加在3的左上变为9，此情况下等式不成立。

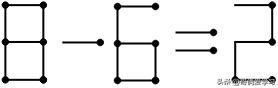
答案5

若8变化： 8只能拿走一根火柴（加号变减号已经拿走一根）且5和3只能在原样子基础上增加火柴或者保持不变。8能变的数是9、6、0：

8变为9时：5只能变为9、8、6或者不变。①当5变为9，3不能通过移动一根火柴变为0，不成立；②当5变为8,没有可移动的火柴，3只能保持不变，不成立；③若5变为6，还剩1根火柴需要加到3上，不成立；④若5不变，3不能通过增加2根火柴变为4，不成立。

8变为6时：5只能变为6或者不变。①若5变为6，3不能通过增加一根火柴变为0，不成立；②若5不变，3不能通过增加两根火柴变为1，不成立；

8变为0时：被减数不够减，不成立。

3.等号右边变化：

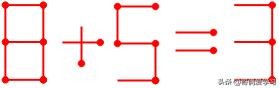
例题2

3.1等号右边变大：最多移动2根火柴的情况下，3变大只能变为5、6、8、9和13。

3变为5时：可假定由3平移右上竖线火柴得到，剩下1根的只能移动等号左边的火柴。加法肯定不行，只能用减法，拿走加号的一根火柴，只能放到5上面，不管5是变为9还是6，等式均不成立；

3变为6时：只能是由3右上竖线火柴平移到左上，然后等号左边移过来一根，很容易清楚，此情况下无答案；

3变为8时：需要从等号左边移过来两根火柴到等号右边。此情况下加号只能不变（若变为减号，算式结果不能等于8），既然结果等于8，左边的数字8肯定要变小，只能变小为6、5、3、2、0。①8变为6，移动了一根火柴，剩下的5无法通过移动一根火柴变为2，不成立；②8变为5,5不能再变，不成立；③8变为3，刚好5不变，等式成立，答案为：3+5=8；④8变为2,5无法再改变，等式不成立，不成立；⑤8变为0,5不能通过移动一根火柴变为8，不成立；

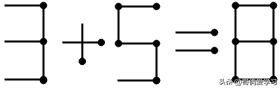
答案6

3变为9时：同理，加号只能保持不变，因此8也只能减小或保持不变，即为8、6、5、3、2、0。①若8不变，5不能通过移动两个火柴变为1，不成立；②若8变为6,5可以将左上竖着火柴平移至右上变为3，6+3=9，等式成立；③若8变为5,5无法通过增加一根火柴变为4，不成立；④若8变为3,5增加一根火柴可变为6，等式成立，答案为：3+6=9；⑤若8变为2,5无法通过增加一根火柴变为7，不成立；⑥若8变为0,5无法通过移动一根火柴变为9，不成立。

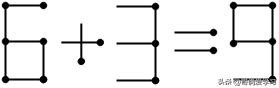
答案7

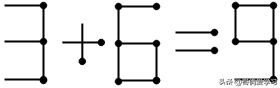
答案8

3变为13时：需要从等号左边移动2根火柴至等号右边，左边加号只能保持不变。8只能变化（若8不变，则5也必须不变才能等于13，不满足条件），即9、6、5、3、2、0；①若8变为9,5不能通过减少一根火柴变为4，不成立；②若8变为6,5不能通过减少一根火柴变为7，不成立；③若8变为5或者3或者2,5都只能不变，三种情况下等式均不成立；④若8变为0,5无法通过减少一根火柴的情况变为13，不成立；

3.2等号右边变小：

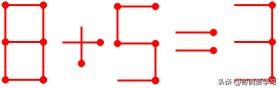
例题2

最多移动2根火柴的情况下，3只能变小为2，那么加号必须变为减号，3变为2可以将右下竖着火柴平移至左下即可，加号变为减号产生的一根火柴只能放在5上，可知当5变为6时，等式成立，即答案为：

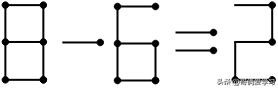
答案9

因此，例题2的所有答案为：8=5+3；6+3=9；3+6=9；8-6=2。

思路总结：

综上，移动火柴类题目，解题思路是多样的，由于本文需要将每个维度的思路解释清楚，故篇幅较长，学生学习的时候，选择一个方向进行探讨即可。

创作不易，如果您觉得还不错，或关注、或评论、或点赞、或分享、或收藏，您的每一个支持都是我继续分享的极大动力，感谢支持！

或关注、或评论、或点赞、或分享、或收藏！！！