适合自学的微积分教材(在家自学微积分)
适合自学的微积分教材(在家自学微积分)
最近因为疫情的关系,很多学校都推迟了开学时间,或者改成了网上教学。对于很多学生来说,在众多课程中,微积分是绕不过的一科。即使被虐千万遍,也依然要待它如初恋……

下面这段历史也许能帮你坚定学习微积分的决心:1665 年,伦敦爆发鼠疫,剑桥大学关闭,一位年轻人不得不返回家乡,在家乡的两年中,他主要研究了微积分、万有引力定律和光学,这些理论对后世产生了巨大的影响,而这个年轻人正是我们所熟知的牛顿大神。

当然,绝大部分人不可能像牛顿那样在疫情期间研究出举世闻名的理论,不过至少,我们可以在这段时间学习一下牛顿留给我们的数学遗产——微积分。
“工欲善其事,必先利其器”,今天推荐的就是一本能够助大家学好微积分,被读者誉为“0 基础也能看懂的高等数学书”——《普林斯顿微积分读本》!
豆瓣 9.6 分高分评价:

这本书讲什么?
这本经典著作源于风靡美国普林斯顿大学的阿德里安·班纳教授的微积分复习课程,将易用性与可读性以及内容的深度与数学的严谨完美地结合在了一起,激励学生不再惧怕微积分,并在考试中获得高分。
本书阐述了求解微积分的技巧,详细讲解了微积分基础、极限、连续、微分、导数的应用、积分、无穷级数、泰勒级数与幂级数等内容,旨在教会读者如何思考问题从而找到解题所需的知识点,着重训练大家自己解答问题的能力。

阿德里安·班纳教授
作者有话说:这本书旨在帮助你学习单变量微积分的主要概念, 同时也致力于教会你求解问题的技巧。无论你是第一次接触微积分, 还是为了准备一次测验, 或是已经学过微积分还想再温习一遍, 我都希望本书能够对你有所帮助。
写作本书的灵感来自我在普林斯顿大学的学生们。他们在过去的几年里发现, 与课堂授课、作业讲解以及他们的教科书一样, 本书的初稿是很有帮助的学习指南。以下是他们在学习过程中提出的一些你可能也想问的问题。
这本书为什么这么厚?(668 页) 我是假设你真的想要掌握这门课程, 而不只是想囫囵吞枣, 一知半解, 所以你已经准备好投入一些时间和精力, 去阅读并理解这些详尽的阐述。
阅读之前, 我需要知道些什么?你需要了解一些基本的代数知识, 并且要知道如何求解简单的方程式。本书的前两章涵盖了你所需要的大部分的微积分预备知识。
例题的求解过程在哪里?我所看到的只是大量的文字与少量的公式。 首先, 看一个求解过程并不能教会你应该怎样思考。所以我通常试图给出一种“内心独白”, 即当你尝试求解问题的时候, 脑海中应该经历怎样的思考过程。最后, 你想到了求解问题的所有知识点, 但仍然需要用正确的方式把它们全部写出来。我的建议是, 先看懂并理解问题的求解方法, 然后再返回来尝试自己解答。
定理的证明哪儿去了?本书中的大部分定理都以某种方式被验证了,在附录 A 中可以找到更多正式的证明过程。
主题没有次序! 我该怎么办呢?学习微积分没有什么标准次序。我选择的顺序是有效的, 但你可能还得通过搜索目录来查找你需要的主题, 我也可能遗漏了一些主题,大家可以给我发邮件:地址是 adrian@calclifesaver.com。你一定想不到, 我可能会为你写一个附加章节。(也为下一版写, 如果有的话!)
我们学校可以用这本书作为教材吗?这本书配有很好的习题集, 可以作为一本教材, 也可以用作一本学习指南,你的任课老师也会发现这本书很有助于备课, 特别是在问题求解的技巧方面。
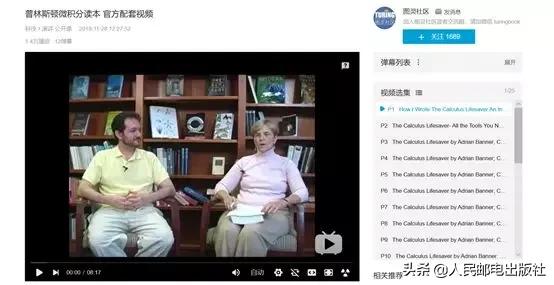
这些视频是什么?这些视频是我过去复习课的录像, 其中涉及了很多 (但不是全部)本书的章节和例题。
班纳教授的复习课视频,B 站可看,点击「链接」可跳转观看
来看看读过的读者怎么说:






《普林斯顿微积分读本》目录如下:

第1章函数、图像和直线1
1.1函数1
1.2反函数6
1.3函数的复合10
1.4奇函数和偶函数12
1.5线性函数的图像14
1.6常见函数及其图像16
第2章三角学回顾21
2.1基本知识21
2.2扩展三角函数定义域23
2.3三角函数的图像29
2.4三角恒等式32
第3章极限导论34
3.1极限:基本思想34
3.2左极限与右极限36
3.3何时不存在极限37
3.4在∞和-∞处的极限38
3.5关于渐近线的两个常见误解41
3.6三明治定理43
3.7极限的基本类型小结45
第4章求解多项式的极限问题47
4.1x → a时的有理函数的极限47
4.2x → a时的平方根的极限50
4.3x → ∞时的有理函数的极限51
4.4x → ∞时的多项式型函数的极限56
4.5x → -∞时的有理函数的极限59
4.6包含绝对值的函数的极限61
第5章连续性和可导性63
5.1连续性63
5.2可导性71
第6章求解微分问题84
6.1使用定义求导84
6.2用更好的办法求导87
6.3求切线方程98
6.4速度和加速度99
6.5导数伪装的极限101
6.6分段函数的导数103
6.7直接画出导函数的图像106
第7章三角函数的极限和导数111
7.1三角函数的极限111
7.2三角函数的导数124
第8章隐函数求导和相关变化率132
8.1隐函数求导132
8.2相关变化率138
第9章指数函数和对数函数148
9.1基础知识148
9.2e 的定义153
9.3对数函数和指数函数求导158
9.4求解指数函数或对数函数的极限161
9.5取对数求导法169
9.6指数增长和指数衰变173
9.7双曲函数178
第10章反函数和反三角函数181
10.1导数和反函数181
10.2反三角函数187
10.3反双曲函数199
第11章导数和图像202
11.1函数的极值202
11.2罗尔定理206
11.3中值定理209
11.4二阶导数和图像212
11.5对导数为零点的分类215
第12章绘制函数图像219
12.1建立符号表格219
12.2绘制函数图像的全面方法224
12.3例题225
第13章最优化和线性化239
13.1最优化239
13.2线性化249
13.3牛顿法258
第14章洛必达法则及极限问题总结263
14.1洛必达法则263
14.2关于极限的总结273
第15章积分276
15.1求和符号276
15.2位移和面积283
第16章定积分293
16.1基本思想293
16.2定积分的定义297
16.3定积分的性质301
16.4求面积305
16.5估算积分313
16.6积分的平均值和中值定理316
16.7不可积的函数319
第17章微积分基本定理321
17.1用其他函数的积分来表示的函数321
17.2微积分的第一基本定理324
17.3微积分的第二基本定理328
17.4不定积分329
17.5怎样解决问题:微积分的第一基本定理331
17.6怎样解决问题:微积分的第二基本定理336
17.7技术要点344
17.8微积分第一基本定理的证明345
第18章积分的方法I347
18.1换元法347
18.2分部积分法356
18.3部分分式361
第19章积分的方法II 373
19.1应用三角恒等式的积分373
19.2关于三角函数的幂的积分376
19.3关于三角换元法的积分384
19.4积分技巧总结391
第20章反常积分:基本概念393
20.1收敛和发散393
20.2关于无穷区间上的积分398
20.3比较判别法(理论)400
20.4极限比较判别法(理论)402
20.5p 判别法(理论) 405
20.6绝对收敛判别法407
第21章反常积分:如何解题410
21.1如何开始410
21.2积分判别法总结413
21.3常见函数在∞和-∞附近的表现414
21.4常见函数在0附近的表现426
21.5如何应对不在0或1处的瑕点432
第22章数列和级数:基本概念434
22.1数列的收敛和发散434
22.2级数的收敛与发散438
22.3第n项判别法(理论) 442
22.4无穷级数和反常积分的性质443
22.5级数的新判别法447
第23章求解级数问题455
23.1求几何级数的值455
23.2应用第n项判别法457
23.3应用比式判别法457
23.4应用根式判别法461
23.5应用积分判别法462
23.6应用比较判别法、极限比较判别法和p判别法463
23.7应对含负项的级数468
第24章泰勒多项式、泰勒级数和幂级数导论472
24.1近似值和泰勒多项式472
24.2幂级数和泰勒级数478
24.3一个有用的极限485
第25章求解估算问题487
25.1泰勒多项式与泰勒级数总结487
25.2求泰勒多项式与泰勒级数488
25.3用误差项估算问题491
25.4误差估算的另一种方法499
第26章泰勒级数和幂级数:如何解题502
26.1幂级数的收敛性502
26.2合成新的泰勒级数508
26.3利用幂级数和泰勒级数求导517
26.4利用麦克劳林级数求极限519
第27章参数方程和极坐标523
27.1参数方程523
27.2极坐标528
第28章复数538
28.1基础538
28.2复平面541
28.3复数的高次幂544
28.4解zn = w 545
28.5解ez = w 550
28.6一些三角级数552
28.7欧拉恒等式和幂级数554
第29章体积、弧长和表面积556
29.1旋转体的体积556
29.2一般立体体积567
29.3弧长571
29.4旋转体的表面积574
第30章微分方程578
30.1微分方程导论578
30.2可分离变量的一阶微分方程579
30.3一阶线性方程581
30.4常系数微分方程585
30.5微分方程建模595
附录A极限及其证明598
A.1极限的正式定义598
A.2由原极限产生新极限602
A.3极限的其他情形606
A.4连续与极限611
A.5再谈指数函数和对数函数616
A.6微分与极限618
A.7泰勒近似定理的证明627
附录B估算积分629
B.1使用条纹估算积分629
B.2梯形法则632
B.3辛普森法则634
B.4近似的误差

有了这本“利器”,希望大家在这段时间能够学好微积分。在疫情结束之前,我们还是不能放松警惕,希望大家能少聚集,勤洗手,多读书,多思考,说不定,你就是下一个牛顿!
,-
- 建阳干货批发市场进货渠道 重庆干货批发市场进货渠道
-
2026-01-31 19:17:19
-

- 非物质文化遗产是什么意思
-
2026-01-31 19:15:05
-

- 赵露思多少岁(赵露思减肥方法)
-
2026-01-31 07:32:18
-
- 男生分手后想复合怎么办(你知道正确的复合方法吗)
-
2026-01-31 07:30:04
-

- 奥黛丽赫本和玛丽莲梦露有哪些区别?
-
2026-01-31 07:27:50
-

- 我的理想高中作文600字,我的理想高中作文300字
-
2026-01-31 07:25:36
-
- 苹果供应商Pegatron开始在印度组装 iPhone 14
-
2026-01-29 19:48:02
-
- 性格相同的人可以在一起吗(性格脾气相似的两个人)
-
2026-01-29 12:20:30
-
- 计算机科学与技术专业就业方向
-
2026-01-29 12:18:16
-

- 吵架了女朋友咬我什么意思
-
2026-01-29 12:16:01
-
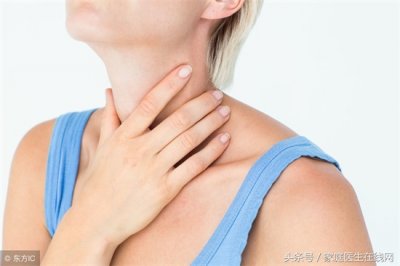
- 16个小方法缓解喉咙痛
-
2026-01-29 12:13:47
-

- 什么是商务谈判
-
2026-01-29 12:11:33
-

- 如何看待婚前试爱(婚前试爱究竟好不好)
-
2026-01-29 12:09:19
-

- 瓶盖创意手工教程,小小瓶盖大变身!
-
2026-01-29 12:07:04
-

- 刘涛新剧《拼图》什么时间播 哪里可以看
-
2026-01-29 12:04:50
-

- 红斑狼疮能治愈吗 患病后可以治愈吗?
-
2026-01-29 12:02:36
-

- 分手后什么时候最难受 分手后怎样让他联系你
-
2026-01-29 12:00:21
-

- 揭阳市有多少常住人口(揭阳各区县人口排名)
-
2026-01-29 05:06:07
-
- 公司会议活动暖场创意-让现场更加生动有趣,强烈推荐
-
2026-01-29 05:03:53
-

- 王老吉与加多宝的爱恨九年,14 亿赔偿还有反转?
-
2026-01-29 05:01:38



 古代女人为什么会肛裂死
古代女人为什么会肛裂死 怎样用棉绳把自己手反绑
怎样用棉绳把自己手反绑